Esboço Do Grafico Da Função Seno E Cosseno Com Exemplo – Esboço Do Gráfico Da Função Seno E Cosseno Com Exemplo é uma ferramenta fundamental para entender o comportamento das funções seno e cosseno, que desempenham um papel crucial em diversas áreas da matemática, física e engenharia. Este guia aborda os conceitos básicos, as etapas para esboçar os gráficos e as aplicações práticas dessas funções, fornecendo exemplos para ilustrar os conceitos e facilitar a compreensão.
Ao dominar o esboço do gráfico da função seno e cosseno, você estará apto a analisar e interpretar fenômenos periódicos, como ondas sonoras, movimento harmônico simples e oscilações em circuitos elétricos. O conhecimento da amplitude, período e fase dessas funções permite a modelagem precisa de diversos sistemas, abrindo portas para uma compreensão mais profunda de seu comportamento.
Introdução ao Gráfico da Função Seno e Cosseno
As funções seno e cosseno são funções trigonométricas fundamentais que desempenham um papel crucial em diversos campos, incluindo matemática, física, engenharia e ciência da computação. Compreender o gráfico dessas funções é essencial para analisar e interpretar fenômenos periódicos que ocorrem na natureza e em sistemas artificiais.
Definição das Funções Seno e Cosseno
A função seno (sen(x)) e a função cosseno (cos(x)) são definidas em relação a um círculo unitário, que é um círculo com raio 1 centrado na origem de um sistema de coordenadas cartesianas. Para um ângulo θ medido no sentido anti-horário a partir do eixo x positivo, sen(θ) é a ordenada do ponto onde a linha que forma o ângulo θ intersecta o círculo unitário, enquanto cos(θ) é a abscissa desse ponto.
Importância de Entender o Gráfico
O gráfico das funções seno e cosseno fornece uma representação visual do comportamento dessas funções, permitindo que se identifiquem padrões, propriedades e relações importantes. Essas informações são essenciais para:
- Resolver equações trigonométricas e encontrar soluções para problemas relacionados a ângulos e triângulos.
- Modelar e analisar fenômenos periódicos, como ondas sonoras, ondas eletromagnéticas e movimento harmônico simples.
- Compreender a teoria de Fourier, que permite decompor funções periódicas em uma soma de funções seno e cosseno.
Características do Gráfico da Função Seno
O gráfico da função seno é uma curva periódica que oscila entre -1 e 1. As principais características do gráfico são:
- Amplitude:A amplitude do gráfico da função seno é a distância vertical máxima entre o eixo x e o ponto mais alto ou mais baixo da curva. A amplitude é representada pela constante “a” na equação geral y = a sen(bx + c).
- Período:O período do gráfico da função seno é o comprimento horizontal de um ciclo completo da curva. O período é calculado como 2π/b, onde “b” é a constante que multiplica “x” na equação geral. O período representa o tempo necessário para que a função complete um ciclo completo.
- Fase:A fase do gráfico da função seno é o deslocamento horizontal da curva em relação ao gráfico da função seno básica y = sen(x). A fase é representada pela constante “c” na equação geral. Um valor positivo de “c” desloca o gráfico para a esquerda, enquanto um valor negativo o desloca para a direita.
Características do Gráfico da Função Cosseno
O gráfico da função cosseno também é uma curva periódica que oscila entre -1 e 1. As principais características do gráfico são semelhantes às da função seno, com algumas diferenças:
- Amplitude:A amplitude do gráfico da função cosseno é a distância vertical máxima entre o eixo x e o ponto mais alto ou mais baixo da curva. A amplitude é representada pela constante “a” na equação geral y = a cos(bx + c).
- Período:O período do gráfico da função cosseno é o comprimento horizontal de um ciclo completo da curva. O período é calculado como 2π/b, onde “b” é a constante que multiplica “x” na equação geral.
- Fase:A fase do gráfico da função cosseno é o deslocamento horizontal da curva em relação ao gráfico da função cosseno básica y = cos(x). A fase é representada pela constante “c” na equação geral. Um valor positivo de “c” desloca o gráfico para a esquerda, enquanto um valor negativo o desloca para a direita.
Esboçando o Gráfico da Função Seno: Esboço Do Grafico Da Função Seno E Cosseno Com Exemplo
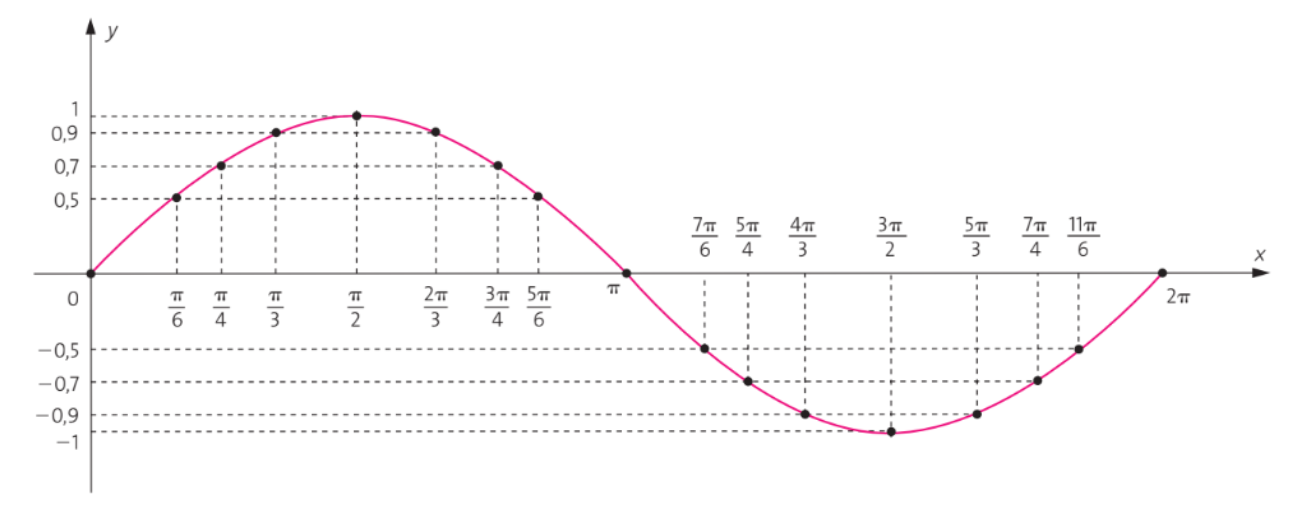
Determinando Amplitude, Período e Fase
Para esboçar o gráfico da função seno, é necessário determinar a amplitude, o período e a fase da função a partir da sua equação. A equação geral da função seno é y = a sen(bx + c), onde:
- “a” representa a amplitude.
- “b” representa a frequência angular, que determina o período (período = 2π/b).
- “c” representa a fase.
Passos para Esboçar o Gráfico da Função Seno
Para esboçar o gráfico da função seno, siga os seguintes passos:
- Identifique a amplitude, o período e a fase da função a partir da sua equação.
- Desenhe o eixo x e o eixo y.
- Determine o período da função e marque pontos chave ao longo do eixo x, correspondentes a um ciclo completo da função.
- Determine a amplitude da função e marque os pontos mais altos e mais baixos da curva.
- Determine a fase da função e desloque o gráfico da função seno básica y = sen(x) para a esquerda ou para a direita, conforme necessário.
- Conecte os pontos chave com uma curva suave, criando o gráfico da função seno.
Exemplo: Esboçando o Gráfico da Função Seno y = 2sen(x + π/4)
Neste exemplo, a amplitude é 2, o período é 2π e a fase é -π/ 4. Para esboçar o gráfico, siga os passos descritos acima:
- Amplitude: 2
- Período: 2π
- Fase:
π/4
- Desenhe o eixo x e o eixo y.
- Marque pontos chave ao longo do eixo x, correspondentes a um ciclo completo da função, com espaçamento de π/2 (período dividido por 4).
- Marque os pontos mais altos e mais baixos da curva, que estão a uma distância de 2 unidades do eixo x (amplitude).
- Desloque o gráfico da função seno básica y = sen(x) para a esquerda em π/4 unidades (fase negativa).
- Conecte os pontos chave com uma curva suave, criando o gráfico da função seno y = 2sen(x + π/4).
Esboçando o Gráfico da Função Cosseno
Determinando Amplitude, Período e Fase
Para esboçar o gráfico da função cosseno, é necessário determinar a amplitude, o período e a fase da função a partir da sua equação. A equação geral da função cosseno é y = a cos(bx + c), onde:
- “a” representa a amplitude.
- “b” representa a frequência angular, que determina o período (período = 2π/b).
- “c” representa a fase.
Passos para Esboçar o Gráfico da Função Cosseno
Para esboçar o gráfico da função cosseno, siga os seguintes passos:
- Identifique a amplitude, o período e a fase da função a partir da sua equação.
- Desenhe o eixo x e o eixo y.
- Determine o período da função e marque pontos chave ao longo do eixo x, correspondentes a um ciclo completo da função.
- Determine a amplitude da função e marque os pontos mais altos e mais baixos da curva.
- Determine a fase da função e desloque o gráfico da função cosseno básica y = cos(x) para a esquerda ou para a direita, conforme necessário.
- Conecte os pontos chave com uma curva suave, criando o gráfico da função cosseno.
Exemplo: Esboçando o Gráfico da Função Cosseno y =
- 3cos(2x
- π/2)
Neste exemplo, a amplitude é 3, o período é π e a fase é π/ 4. Para esboçar o gráfico, siga os passos descritos acima:
- Amplitude: 3
- Período: π
- Fase: π/4
- Desenhe o eixo x e o eixo y.
- Marque pontos chave ao longo do eixo x, correspondentes a um ciclo completo da função, com espaçamento de π/4 (período dividido por 4).
- Marque os pontos mais altos e mais baixos da curva, que estão a uma distância de 3 unidades do eixo x (amplitude).
- Desloque o gráfico da função cosseno básica y = cos(x) para a direita em π/4 unidades (fase positiva).
- Conecte os pontos chave com uma curva suave, criando o gráfico da função cosseno y =
- 3cos(2x
- π/2).
Comparando os Gráficos da Função Seno e Cosseno
Comparando e Contrastando Características
Os gráficos das funções seno e cosseno compartilham algumas características, mas também apresentam diferenças importantes:
- Posição Inicial:O gráfico da função seno começa na origem (0, 0), enquanto o gráfico da função cosseno começa no ponto (0, 1).
- Comportamento em Relação ao Eixo x:O gráfico da função seno cruza o eixo x nos pontos múltiplos de π, enquanto o gráfico da função cosseno cruza o eixo x nos pontos múltiplos de π/2.
- Relação entre os Gráficos:O gráfico da função cosseno pode ser obtido deslocando o gráfico da função seno para a esquerda em π/2 unidades. Ou seja, cos(x) = sen(x + π/2).
Transformações entre as Funções
As funções seno e cosseno podem ser transformadas uma na outra através de translações e reflexões. Por exemplo, a função y = sen(x) pode ser transformada na função y = cos(x) deslocando-a para a esquerda em π/2 unidades. Da mesma forma, a função y = cos(x) pode ser transformada na função y = sen(x) deslocando-a para a direita em π/2 unidades.
Aplicações do Gráfico da Função Seno e Cosseno
Física
Os gráficos da função seno e cosseno são amplamente utilizados em física para descrever fenômenos periódicos, como:
- Ondas Sonoras:As ondas sonoras são ondas longitudinais que se propagam através de um meio, como o ar, causando variações na pressão do ar. Essas variações de pressão podem ser modeladas por funções seno ou cosseno.
- Ondas Eletromagnéticas:As ondas eletromagnéticas são ondas transversais que se propagam através do espaço, transportando energia. O campo elétrico e o campo magnético associados a essas ondas podem ser descritos por funções seno ou cosseno.
- Movimento Harmônico Simples:O movimento harmônico simples é um tipo de movimento periódico em que um objeto oscila em torno de uma posição de equilíbrio, como um pêndulo ou uma mola. A posição, a velocidade e a aceleração do objeto podem ser descritas por funções seno ou cosseno.
Engenharia
Os gráficos da função seno e cosseno também são utilizados em engenharia para modelar oscilações em diversos sistemas, como:
- Circuitos Elétricos:As correntes e as tensões em circuitos elétricos AC (corrente alternada) podem ser modeladas por funções seno ou cosseno.
- Sistemas Mecânicos:Oscilações em sistemas mecânicos, como vibrações em pontes ou edifícios, podem ser modeladas por funções seno ou cosseno.
Matemática

Os gráficos da função seno e cosseno desempenham um papel fundamental em diversos ramos da matemática, incluindo:
- Teoria de Fourier:A teoria de Fourier permite decompor funções periódicas em uma soma de funções seno e cosseno, o que é essencial para análise de sinais e processamento de sinais.
- Análise de Sinais:Os gráficos da função seno e cosseno são utilizados para analisar e interpretar sinais periódicos, como sinais de áudio, sinais de vídeo e sinais de comunicação.

