Exercícios Sobre O Gráfico Da Função Do Segundo Grau: embarque numa jornada fascinante pelo mundo das parábolas! Descubra os segredos por trás das curvas elegantes que representam as funções quadráticas. Prepare-se para desvendar os mistérios dos coeficientes, vértices e raízes, dominando a arte de interpretar gráficos e solucionar problemas do mundo real com a elegância matemática das funções do segundo grau.
Nesta exploração, você não apenas resolverá equações, mas também construirá uma compreensão profunda e intuitiva do comportamento dessas funções tão presentes em diversas áreas da ciência e da engenharia.
Aprenderemos a decifrar a linguagem visual das parábolas, compreendendo como cada elemento da equação – os coeficientes a, b e c – molda a forma e a posição do gráfico. Exploraremos técnicas para encontrar o vértice, as raízes e o eixo de simetria, tanto algebricamente quanto através da análise visual do gráfico. Veremos como aplicar esses conhecimentos na resolução de problemas práticos, desde o cálculo de áreas até a modelagem da trajetória de um projétil.
Prepare-se para uma aventura matemática que irá expandir seus horizontes e fortalecer suas habilidades analíticas!
Análise do Gráfico da Função do Segundo Grau: Exercícios Sobre O Gráfico Da Função Do Segundo Grau
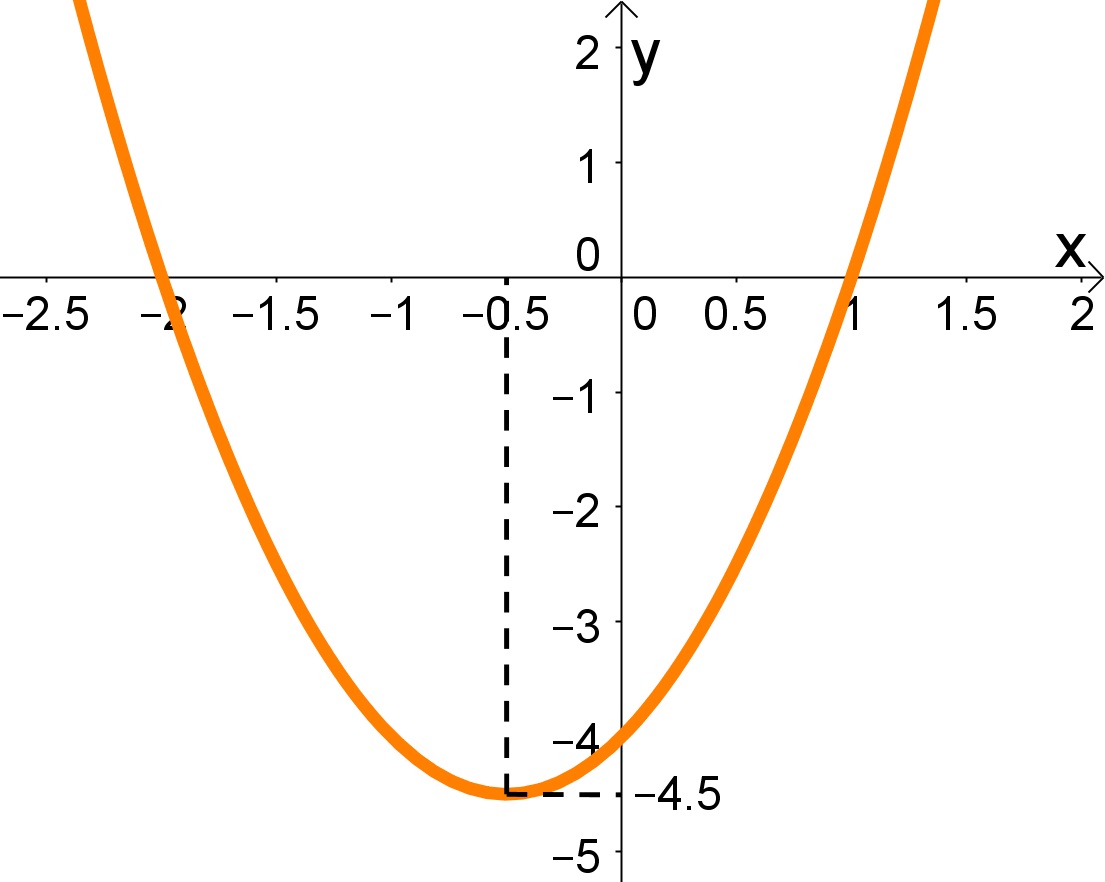
A jornada pela compreensão das funções quadráticas nos leva a um território fascinante: a análise de seus gráficos, as parábolas. Esses gráficos, aparentemente simples em sua forma curvilínea, escondem uma riqueza de informações sobre o comportamento da função, revelando seus segredos através de suas características geométricas. Preparar-se para decifrar essas informações é o primeiro passo para dominar o mundo das funções do segundo grau.
Comparação de Gráficos com Diferentes Valores de ‘a’

O coeficiente ‘a’ na equação da função quadrática, f(x) = ax² + bx + c
, desempenha um papel crucial na forma da parábola. Se ‘a’ for positivo, a parábola se abre para cima, indicando um ponto mínimo; se ‘a’ for negativo, ela se abre para baixo, indicando um ponto máximo. A magnitude de ‘a’ também influencia a abertura da parábola: quanto maior o valor absoluto de ‘a’, mais fechada será a parábola; quanto menor, mais aberta.
Imagine duas parábolas, uma com a=2 e outra com a=0.5. A primeira será mais fechada e estreita, enquanto a segunda será mais aberta e larga, ilustrando como o coeficiente ‘a’ molda a forma da curva.
Identificação do Eixo de Simetria

O eixo de simetria é uma reta vertical que divide a parábola em duas metades congruentes, espelhadas uma em relação à outra. Sua equação é dada por x = -b/2a
. Geometricamente, o eixo de simetria passa pelo vértice da parábola, ponto de coordenada x igual a -b/2a. Observando o gráfico, basta identificar o ponto médio entre as duas raízes (ou o ponto mais alto/baixo da parábola, se não houver raízes reais), e traçar uma reta vertical que passa por esse ponto.
Essa reta representa o eixo de simetria. Imagine uma parábola perfeita, como um arco de ponte: o eixo de simetria seria a linha imaginária que corta o arco exatamente no meio.
Determinação do Valor Máximo ou Mínimo
O vértice da parábola representa o ponto de máximo ou mínimo da função. Se a parábola se abre para cima (a>0), o vértice representa o ponto de mínimo; se se abre para baixo (a <0), representa o ponto de máximo. O valor máximo ou mínimo corresponde à coordenada y do vértice. Observando o gráfico, basta identificar a coordenada y do ponto mais alto ou mais baixo da parábola para determinar o valor máximo ou mínimo da função. Por exemplo, se o vértice está em (2, -1), o valor mínimo da função é -1.
Encontrar as Raízes da Função
As raízes da função, também conhecidas como zeros ou interseções com o eixo x, são os valores de x para os quais f(x) = 0.
Graficamente, são os pontos onde a parábola intersecta o eixo x. Se a parábola não interceptar o eixo x, a função não possui raízes reais. Observando o gráfico, basta identificar os pontos onde a curva cruza o eixo horizontal (eixo x). As coordenadas x desses pontos representam as raízes da função.
Exemplo: Encontrando Coordenadas do Vértice e Raízes a Partir de um Gráfico
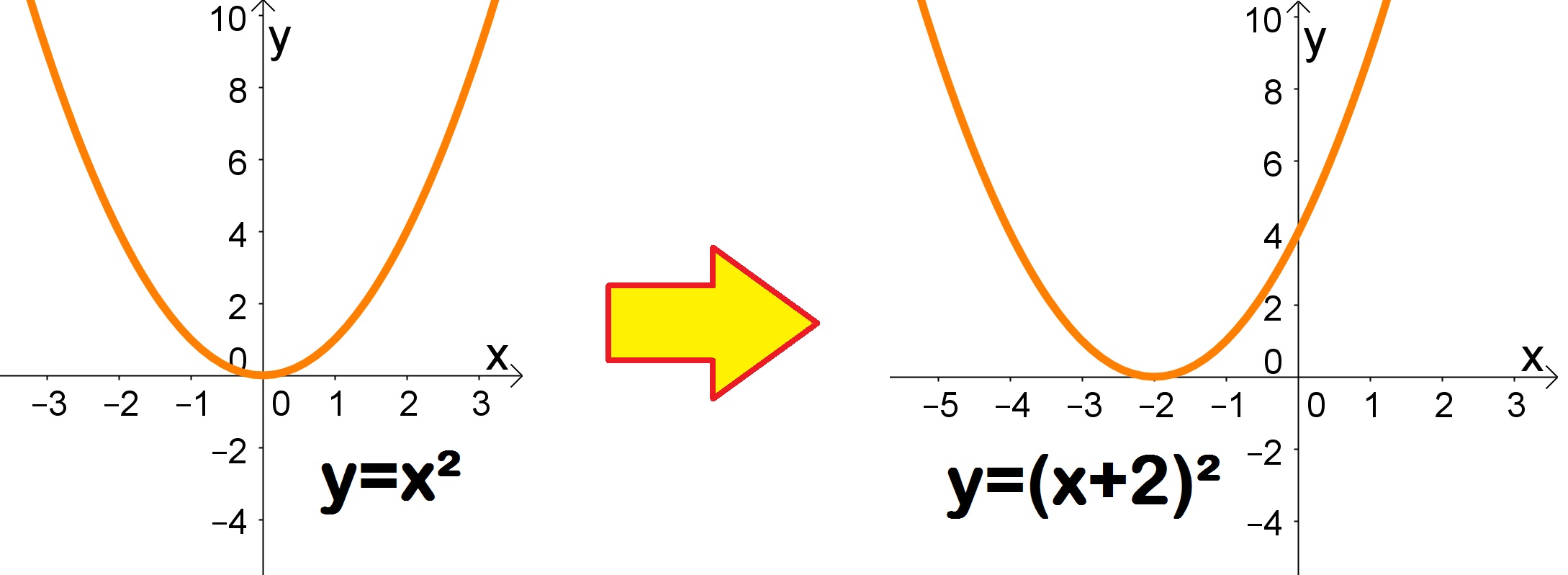
Imagine um gráfico mostrando uma parábola que intersecta o eixo x em x = 1 e x = 5, e cujo ponto mais baixo (vértice) está em (3, -4).
- Identificação das raízes: O gráfico mostra que a parábola intersecta o eixo x em x = 1 e x = 5. Portanto, as raízes da função são 1 e 5.
- Determinação do eixo de simetria: O eixo de simetria está localizado no ponto médio entre as raízes. (1+5)/2 = 3. Logo, a equação do eixo de simetria é x = 3.
- Identificação das coordenadas do vértice: O gráfico mostra que o vértice está localizado em (3, -4).
- Conclusão: As raízes da função são 1 e 5, e as coordenadas do vértice são (3, -4).
Aplicações e Problemas com a Função do Segundo Grau
A função quadrática, com sua elegante curva parabólica, não se limita ao universo abstrato da matemática. Ela encontra aplicações práticas em diversas áreas, modelando fenômenos e resolvendo problemas do mundo real, desde o cálculo de áreas até a previsão da trajetória de um projétil. A capacidade de descrever relações entre variáveis com precisão e elegância a torna uma ferramenta poderosa e versátil.
Um Problema de Modelagem com Função Quadrática
Imagine um fazendeiro que deseja cercar um terreno retangular utilizando 100 metros de cerca. Ele quer maximizar a área do terreno. Podemos modelar essa situação com uma função quadrática. Sejam x e y os lados do retângulo. A equação da cerca é 2x + 2y = 100, simplificando para y = 50 – x.
A área A é dada por A = xy = x(50 – x) = 50x – x². Esta é uma função quadrática, e seu vértice representa a área máxima. Resolvendo a equação do vértice, encontramos x = 25, o que implica y = 25. Portanto, a área máxima é atingida quando o terreno é um quadrado com lados de 25 metros, resultando em uma área de 625 metros quadrados.
Cálculo de Área com Função Quadrática
Um exercício que envolve o cálculo de área utilizando uma função quadrática pode ser proposto da seguinte forma: Determine a área da região delimitada pela curva y = x²4x + 5, o eixo x, e as retas x = 1 e x =
-
4. A área pode ser calculada através da integral definida
∫14 (x²
- 4x + 5) dx
. Resolvendo a integral, encontramos a área da região. Este exercício demonstra a ligação entre o cálculo integral e a geometria, utilizando a função quadrática como elemento central.
Lançamento de um Projétil

A trajetória de um projétil lançado obliquamente pode ser descrita por uma função quadrática da forma h(t) = -4.9t² + vt + h 0, onde h(t) é a altura em função do tempo t, v é a velocidade inicial vertical e h 0 é a altura inicial. Considere um projétil lançado com velocidade inicial vertical de 20 m/s e altura inicial de 1.5 metros.
Sua trajetória é dada por h(t) = -4.9t² + 20t + 1.
- O ponto máximo é o vértice da parábola, que pode ser encontrado utilizando a fórmula do x do vértice:
tv = -b / 2a = -20 / (2
- -4.9) ≈ 2.04 segundos
. Substituindo esse tempo na equação, encontramos a altura máxima.
Resolução de Inequação Quadrática, Exercícios Sobre O Gráfico Da Função Do Segundo Grau
Resolva a inequação x²
- 5x + 6 ≤ 0. Primeiramente, encontramos as raízes da equação x²
- 5x + 6 = 0, que são x = 2 e x = 3. Como o coeficiente de x² é positivo, a parábola abre para cima. Portanto, a inequação é satisfeita para valores de x entre as raízes. Graficamente, a solução é representada pela região abaixo da parábola, entre x = 2 e x = 3, incluindo esses pontos.
Um gráfico mostrando a parábola y = x²
- 5x + 6 com a região sombreada entre x = 2 e x = 3 ilustraria claramente a solução.
Problema de Otimização

Um gráfico representando a solução de um problema de otimização envolvendo uma função quadrática poderia mostrar a receita (y) de uma empresa em função da quantidade de produtos vendidos (x), representada por uma parábola que abre para baixo. O vértice da parábola representa a quantidade de produtos que maximiza a receita.
Legenda:
Eixo X: Quantidade de produtos vendidos
Eixo Y: Receita em Reais
Vértice: Ponto de receita máxima
Região sombreada: Região onde a receita é positiva.
O gráfico mostraria uma parábola com concavidade voltada para baixo, seu vértice representando o ponto de máxima receita. A região sombreada abaixo da curva, acima do eixo x, representaria a região onde a receita é positiva. A abscissa do vértice indicaria a quantidade ideal de produtos a serem vendidos para se obter o lucro máximo.

